Forschungsgegenstand
Forschungsgegenstand sind Ultraschallfelder in Flüssigkeitsströmungen. Schallfelder und Strömungen beeinflussen sich in komplexer Weise gegenseitig, die dabei auftretenden Mechanismen sind teilweise noch nicht geklärt. Viele dabei auftretende Phänomene wie z.B. Kavitation können bis heute nur qualitativ beschrieben werden. Dies liegt u.a. daran, dass die physikalischen Grundgleichungen stark nichtlinear sind und einfache Lösungen nur in seltenen Sonderfällen bekannt sind.
Der Kooperationspartner, die BANDELIN electronic GmbH & Co. KG, stellt Ultraschallgeräte her, die unter anderem in der Lage sind, medizinische Apparate berührungslos zu reinigen; von Interesse ist daher, die Schallverteilung und ihre Aus- und Wechselwirkungen im Voraus zu berechnen, zumal ihre Vermessung wegen der auftretenden Kavitation oder aufgrund der Gefäßgeometrie schwierig oder unmöglich ist.
Forschungsziel
Das Projektziel besteht darin, Ultraschall- und Strömungsfelder in chemischen Reaktoren zu untersuchen und zu optimieren. Für gemeinsam mit dem Kooperationspartner ausgewählte Geräte wie z.B. Sonoreaktoren u.ä.m. sollen im ersten Schritt die auftretenden Schalldruckfelder bestimmt werden. Hierfür werden Standardprogramme wie Comsol Multiphysics eingesetzt.

MODOPUS – Modellierung und Optimierung von Ultraschall und Strömung in der Medizintechnik
Im zweiten Schritt wird der Einfluss der Flüssigkeitsströmung untersucht. Von Interesse sind hier besonders Gebiete mit hohem Schalldruck. Die Schallwandler lassen sich gruppenweise mit einer Phasenverschiebung ansteuern, sodass die am besten geeigneten Ansteuerungsformen gefunden werden können.
Im dritten Schritt wird zusätzlich die Schallabsorption im beschallten Medium berücksichtigt
Methoden
Die zugrundeliegenden Gleichungen lassen sich analog zu den Navier-Stokes-Gleichungen aus den Erhaltungsgesetzen für Masse und Impuls herleiten. Dabei verfolgt man den Ansatz, dass sich Dichte ρ, Druck p und Geschwindigkeit v des Mediums jeweils aus einem stationären Anteil (Index 0) und einem kleineren Wechselanteil (Index ´) zusammensetzen, der sich mit der Schallfrequenz (entweder 25 oder 40 kHz) ändert:
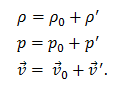
Die Erhaltungsgleichungen lassen sich dann separieren in je eine Gleichung für die stationären Größen (nullter Ordnung) und für die Wechselgrößen (erster Ordnung). In erster Ordnung erhält man für die Erhaltung von Masse und Impuls:
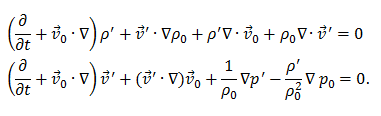
Für wirbelfreie Strömungen schließlich gewinnt man mit der Einführung eines Schallschnellepotentials φ mit
eine skalare Differenzialgleichung für φ:
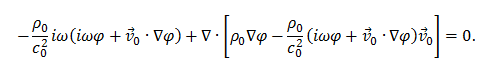
Darin ist die Zeitableitung der zeitharmonischen Größen durch ∂/δt = iω ausgedrückt. Nach Lösung dieser Gleichung mit der Finite-Elemente-Methode erhält man den Schalldruck aus
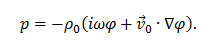
Für die Absorption existieren Ansätze zur Berechnung komplexer Wellenzahlen aus dem Materialparametern des Mediums, z.B. in [3].
Ergebnisse
Es lässt sich der Einfluss der Flüssigkeitsströmung auf das Schallfeld beschreiben, eine exemplarische Darstellung siehe Abbildung 2.
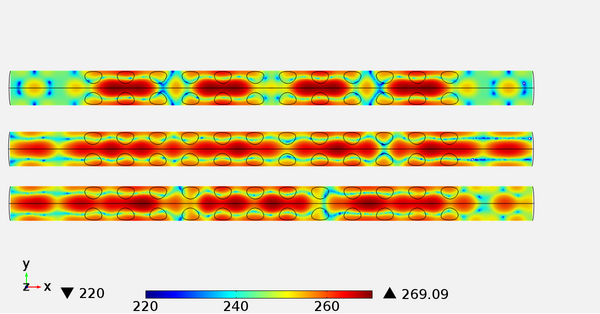
Veröffentlichungen
Die Veröffentlichungen zu diesem Projekt finden Sie hier.
Literatur
[1] Allan D. Pierce: Wave equation for sound in fluids with unsteady inhomogeneous flow, J. Acoust. Soc. Am. 87, 2292 (1990)
[2] M. E. Goldstein: Aeroacoustics, New York, McGraw-Hill International Book Co., 1976.
[3] Lahiri, Claus und Knobloch, Karsten und Bake, Friedrich und Enghardt, Lars (2013) Attenuation of sound in wide ducts with flow at elevated pressure and temperature. In: 19th AIAA/CEAS Aeroacoustics Conference (34th AIAA Aeroacoustics Conference) (AIAA-2013-2072). 19th AIAA/CEAS Aeroacoustics Conference (34th AIAA Aeroacoustics Conference), 27 - 29 May 2013, Berlin, Germany.
