Verwendung der BEM-basierenden Fast Multipole Methode für Innenraumprobleme

(02/2011 - 12/2011)

Abstrakt
Im Rahmen des Forschungsprojekts MULTIPOL wird eine neuartige Variante der Randelementemethode (BEM) für Innenraumprobleme in Kombination mit der Multi-Level Fast-Multipol-Methode (MLFMM) entwickelt, mit deren Hilfe sich Schallfelder in Außen- und Innenräumen auf numerische Weise vorausberechnen lassen.

Veröffentlichungen
Die Veröffentlichungen zu diesem Projekt finden Sie hier.

Förderung
Dieses Projekt wurde durch das Institut für angewandte Forschung Berlin e.V. (IfaF) gefördert.

ifaf_logo_small_web

Zielsetzung
Die numerische Berechnung bzw. Simulation der Schallausbreitung in Innenräumen im mittleren und höheren Frequenzbereich des Hörvermögens ist mit den gängigen konventionellen Methoden aufgrund der Größe der sich ergebenden Gleichungssysteme nur begrenzt möglich, da der Speicherbedarf für die Systemmatrix den verfügbaren Speicher gängiger Workstations schnell übersteigt.

Die Fast-Multipol-Methode stellt ein Verfahren zur beschleu­nigten Bildung eines Matrix-Vektor-Produktes (MVP) dar, ohne dabei jemals die Matrix vollständig erstellen zu müssen. Sie eignet sich daher in Verbindung mit iterativen Lösern zum Einsatz bei großen Gleichungssystemen.

Methodik
Ein Code für einen Multi-Level Fast Multipol Algorithmus wird entsprechend erweitert, optimiert und die erzielten Resultate mit den Ergebnissen von konventionellen matrix­basierenden BEM-Berechnungen und denen kommerzieller FEM-Software (z.B. COMSOL Multiphysics) verglichen.

Zusätzlich wird der Code nach MatLAB portiert, um Untersuchungen zur Optimierung des Algorithmus und des verwendeten iterativen Lösungsverfahrens zu erleichtern.

Randelementmethode
Die Randelementmethode (boundary element method, BEM) hat sich als gängiges Verfahren zur Lösung akustischer Problemstellungen etabliert, da für die numerische Berech­nung nur die Oberfläche der schwingenden Struktur (Abb. 1) berücksichtigt werden muss, die dafür in einzelne kleine Elemente zerlegt („diskretisiert“) wird. Das Volumen des Außen- oder Innenraums geht in die Berechnung nicht ein.

Struktur-nach-BEM
Abb. 1: Zerlegung der Oberfläche einer schwingenden Struktur (Vollkörper, links) in einzelne Elemente (Diskretisierung, rechts, konstante Elemente)

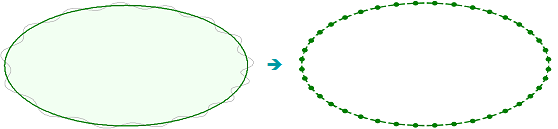
Dies ist ein großer Vorteil der BEM und spiegelt sich in deutlich kleineren Gleichungssystemen wieder, als sie z. B. in der Finiten-Element-Methode (FEM) auftreten. Da jedes Element mit jedem anderen Element interagiert (Abb. 3), ergeben sich voll besetzte komplexe Gleichungssysteme.

Fast-Multipol-Methode
Bei dieser Methode werden die Wirkungen einzelner Quellen zu einem sog. Multipol zusammengefasst. Dieser Vorgang erfolgt für alle Oberflächenelemente, sodass sich eine geometrische Aufteilung in einzelne Cluster ergibt (Abb. 2).

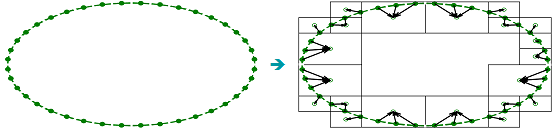
BEM-nach-MLFMM

Die Abnahme der Anzahl der so zu berücksichtigenden Inter­aktionen zwischen den Clustern (Abb. 4) ist im Vergleich mit den direkten Interaktionen (Abb. 3) deutlich erkennbar.

Interaktionen_BEM
Abb. 3: konventionelle Berechnung der Interaktionen
Interaktionen_MLFMM
Abb. 4: Cluster-basierende Interaktionen bei der MLFMM

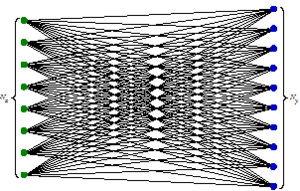
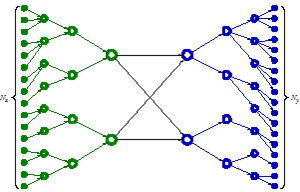
Im dreidimensionalen Fall werden die Cluster durch würfel­förmige Boxen repräsentiert (Abb. 5).

MLFMM_BoxSample
Abb. 5: Beispiel der Interaktionslisten eines MLFMM-Clusters (Box)

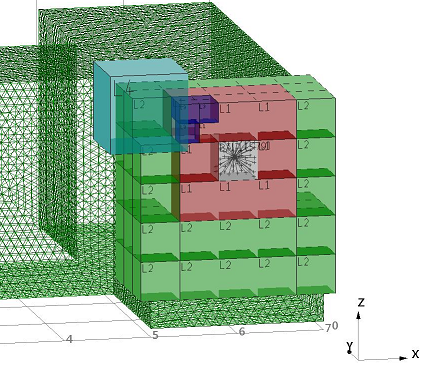
Beispiel I: Schallharte Kugel, 2 m Durchmesser, 100.750 Elemente
Dieses Beispiel zeigt die Ergebnisse und Lösungszeiten der Berechnung der Schalldruckverteilung auf der Oberfläche einer einfachen Kugel und deren Abstrahlung bei verschiedenen Frequenzen.

verwendetete Abkürzungen:

tsolve

Lösungszeit (ohne Pre-/Postprocessing)

Omp

Ordnung der Multipol-Entwicklung

Niter

Anzahl der Iterationen

eiter

max. vorg. Iterationsfehler

GMRES

iterativer Löser (General minimal residuum)

IMKL

Intel Math Kernel Library (direkter Löser)


a) f = 273 Hz (ka = 5)

konventionell:

tsolve:

4.472,0

s [01:14:32]

MLFMM:

tsolve:

24,5

s

 

Omp:

4

... 17

Kugel_2m_100k__Ergebnis_273_Hz__XY-Ebene__Entfernung_5_m_
Abb. 6: schallharte Kugel, f = 100 Hz, Gesamtdruck [Pa] in 5 m Distanz

c) f = 2.730 Hz (ka = 50)

konventionell:

Niter:

140

(eiter < 10-8)

 

tsolve:

45.718

s [12:41:58]

MLFMM:

Niter:

201

(eiter = 1-2), Fehlerlimit nicht erreicht!

 

tsolve:

2.685

s [00:44:45]

 

Omp:

6

... 116

Kugel_2m_100k__Ergebnis_1000_Hz__XY-Ebene__Entfernung_5_m_
Abb. 7: schallharte Kugel, f = 1.000 Hz, Gesamtdruck [Pa] in 5 m Distanz

b) f = 1.000 Hz (ka ≈ 18,3)

konventionell:

tsolve:

19.582

s [05:26:22]

MLFMM:

tsolve:

582

s

 

Omp:

4

... 49

Kugel_2m_100k__Ergebnis_2730_Hz__XY-Ebene__Entfernung_5_m_
Abb. 8: schallharte Kugel, f = 2.730 Hz, Gesamtdruck [Pa] in 5 m Distanz

Ab einer Frequenz von ca. 1 kHz treten erste sichtbare Differenzen im Druckverlauf (Abb. 7) auf, die mit steigender Frequenz deutlich zunehmen (Abb. 8), da der iterative Löser aufgrund der bei der MVP-Bildung verstärkt auftretenden Fehler nicht mehr gut konvergiert.

Beispiel II: T-Raum mit schallharten Wänden und Türbereich
Dieses zeigt die Ergebnisse der FEM und BEM für einen T-förmigen Innenraum von ca. 7 × 3 × 2,5 m Größe mit schall­harten Wänden und einem Türbereich mit der Impedanz ρc.

COMSOL_T-Raum_mit_Tuer_abs_psurf__new
Abb. 9: T-Raum, 250 Hz, FEM-Lösung

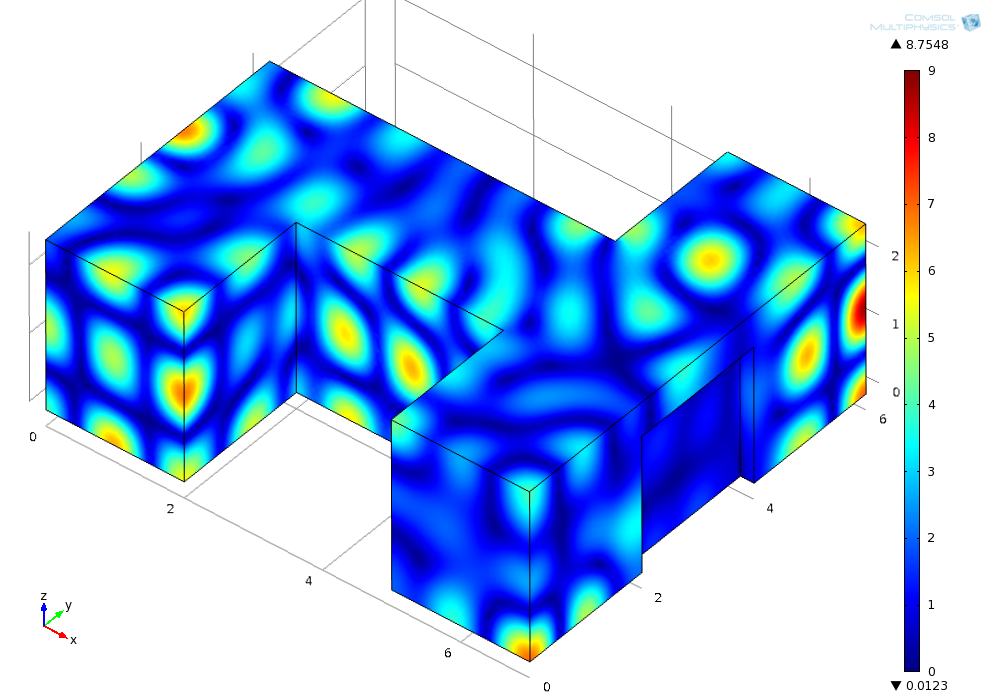
a) FEM-Lösung (COMSOL)

Nelem:

1.093.480

Niter:

14

tsolve:

772

s [01:14:32]

Löser:

MUMPS(sparse iterative solver)

T-Raum_mit_Tuer__30_358_Elemente__MLFMM_P50_M06_U07
Abb. 10: T-Raum, 250 Hz, MLFMM, Omp = 6

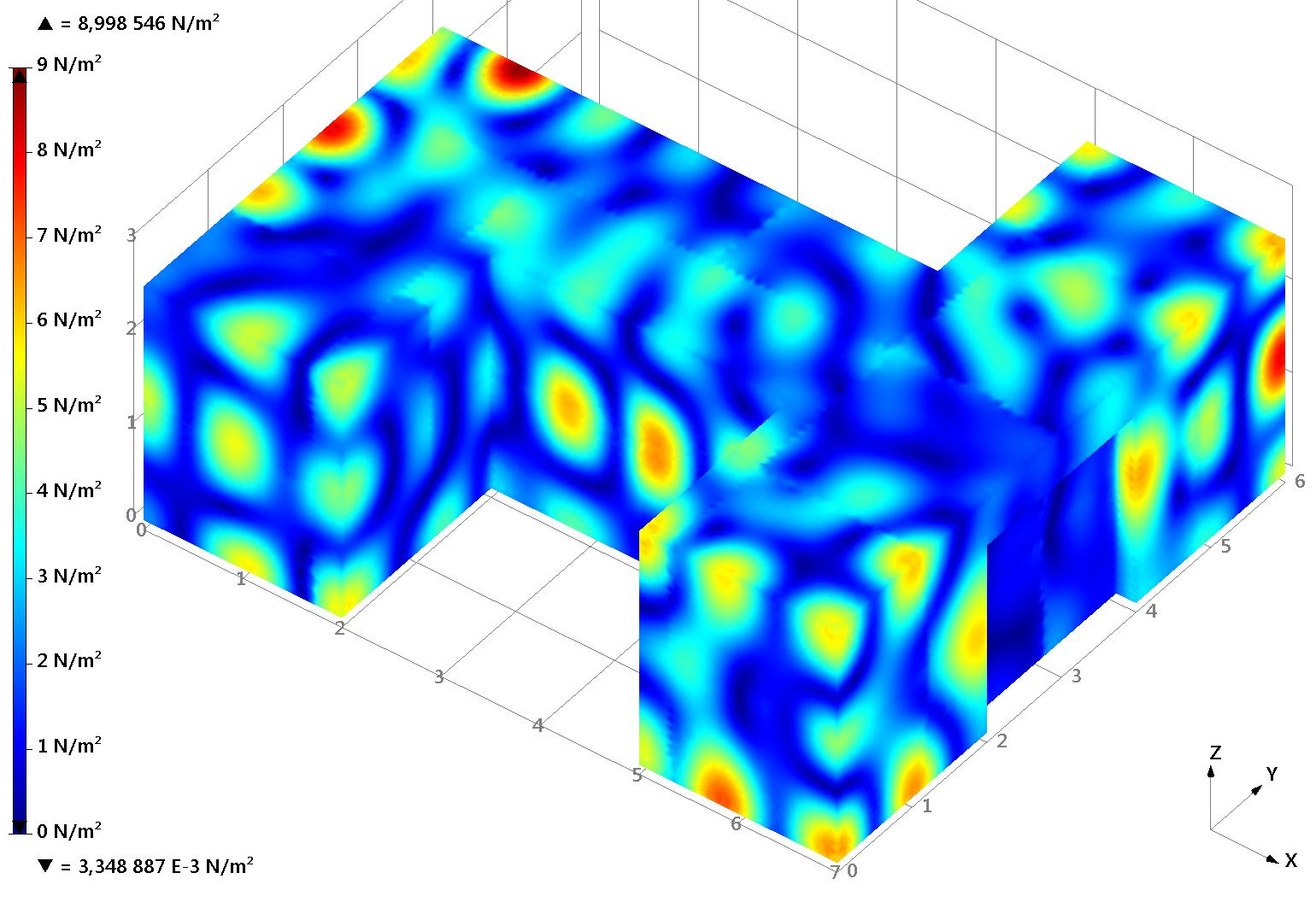
b) BEM mit MLFMM

Nelem:

30.558

Omp:

6

(fest)

Niter:

183

eiter:

< 10-5

tsolve:

116

s

Deutliche Abweichungen des Schalldruckverlaufs an den Clustergrenzen!

T-Raum_mit_Tuer__30_358_Elemente__MLFMM_P50_M10_U11
Abb. 11: T-Raum, 250 Hz, MLFMM, Omp = 10

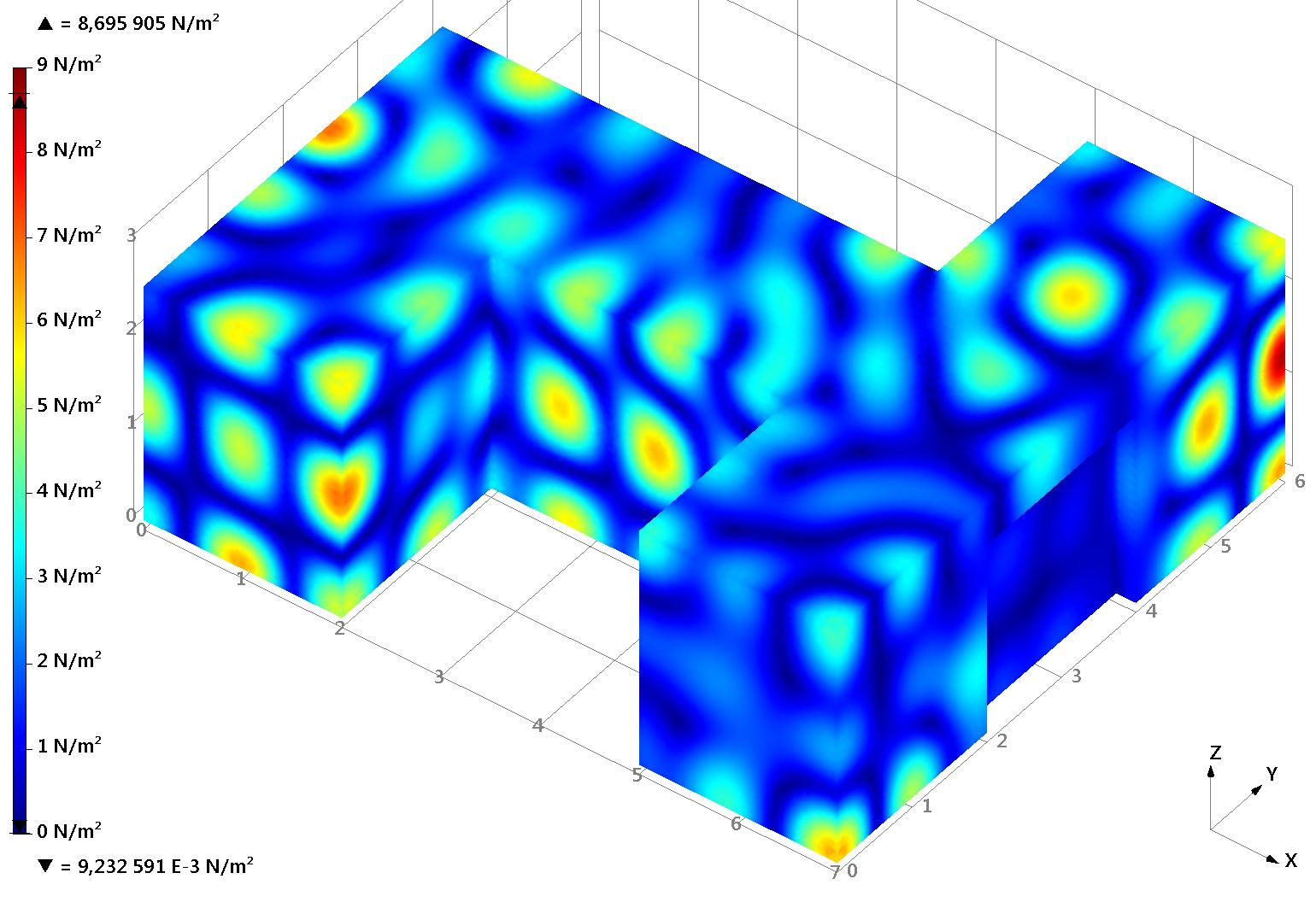
c) BEM mit MLFMM

Nelem:

30.558

Omp:

10

(fest)

Niter:

191

eiter:

< 10-5

tsolve:

291

s


d) BEM (konventionell)

tsolve,GMRES:

204

s

tsolve,IMKL:

710

s

Auch hier ist ist deutlich zu erkennen, wie stark die Qualität der Lösung von der Entwicklungsordnung Omp abhängt.

Fazit
Die dargestellten Ergebnisse zeigen, dass die MLFMM im Vergleich zur konventionellen BEM bei geringeren Rechen­zeiten qualitativ vergleichbare Ergebnisse liefert. Dieser Performancevorteil zeigt sich insbesondere bei komplexeren Strukturen und unterschiedlichen Randbedingungen.

Bei höheren Frequenzen weist die MLFMM jedoch deutliche qualitative Abweichungen auf, da sich die methoden­basierenden Fehler in der Matrix-Vektor-Produktbildung stärker auswirken. Hier sind weitere Untersuchungen zur Optimierung des MLFMM-Codes notwendig. Ebenso soll ein geeigneter Vorkonditionierer verwendet werden, um eine bessere Konvergenz des iterativen Verfahrens zu erzielen.