Berechnung der akustischen Abstrahlung einer offenen turbulenten Flamme durch eine transiente BEM
Ausgangssituation
Die transiente Randelementmethode findet aufgrund von Instabilitätsproblemen und hohem numerischen Aufwand bis jetzt wenig Anwendung in der Akustik. Mit Hilfe der Kirchhoffschen Integralgleichung wird die transiente Schallabstrahlung einer offenen turbulenten Flamme berechnet. Die zur Berechnung nötige Geschwindigkeitsverteilung auf einer zylindrischen Kontrollfläche (Kirchhoff Surface) basiert auf einer Large Eddy Simulation (LES). Verglichen werden die Ergebnisse mit Messdaten und Berechnungen der Randelementmethode im Frequenzbereich.
Ziel des Projektes
Das Ziel dieses Projektes ist der Vergleich von BEM-Berechnungen aus dem Zeit- und Frequenzbereich am konkreten Beispiel einer offenen turbulenten Flamme.
siehe auch "Forschungsprojekte/Combustion Noise"
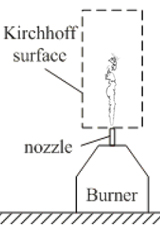
Geschichtlicher Abriss
Die Randelementmethode (BEM für Boundary Element Method) ist ein weit verbreitetes numerisches Verfahren. Für transiente Probleme wird sie meist im Frequenzbereich oder Laplace-Bereich mit anschließender inverser Transformation formuliert. Mansur and Brebbia [1], [2] entwickelten im Zeitbereich eine der ersten BEM-Formeln für die skalare Wellengleichung und für Elastodynamik mit dem Anfangswertproblem zu Null. Die Ausweitung dieser Formulierungen auf Anfangswertprobleme zu ungeich Null wurde von Antes [3] vorgestellt. Später weiteten Jäger [4], Antes and Baaran [5] die Zeitbereichsformeln auf die 3- dimensionale Schallausbreitung von sich bewegenden Quellen aus.
Numerisches Modell
Die allgemein bekannte transiente Randintegralgleichung kann folgendermaßen formuliert werden:
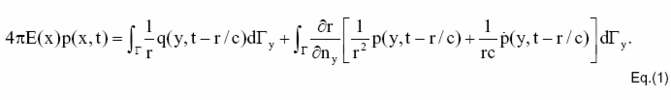
Hier bezeichnet p(x,t) den Schalldruck, r den Abstand zwischen den Punkten x und y, c die Schallausbreitungsgeschwindigkeit, (!!!groß Gamma!!!) die Oberfläche und q(x,t) den Fluss. Die aus der Eulerschen Gleichung hergeleitete Beziehung lautet
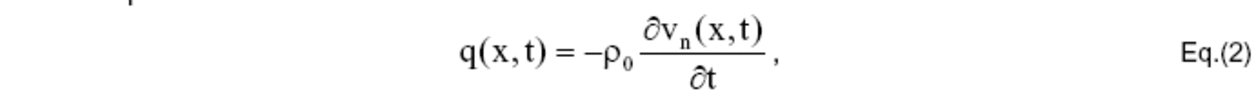
mit vn als Normalenschnelle. E(x) ist definiert als
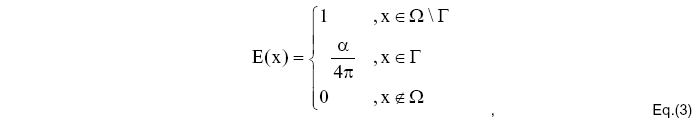
wobei α den inneren festen Winkel bezeichnet und Ω den Bereich. Eine detailierte Herleitung der obigen Randintegralgleichung kann z.B. in Araujo et al. [6] oder Meise [7]gefunden werden.
Um eine zeitdiskrete Version von Gl.(1) zu erhalten, wird für die Zeitableitung ein Rückwärtsdifferenzquotient und für p eine lineare Interpolationsfunktion benutzt.
Die Zeit selbst wird durch equidistante Zeitschritte ti = iδt diskretisiert, und so erhält man für die retadierte Zeit tri = iδt-r/c. Die Geometrie wird in N planare Elemente zerlegt. Gamman (n=1,2,....N) mit einer gleichförmigen Druckverteilung pmn.
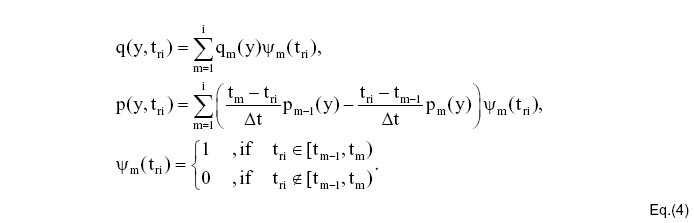
Aus Kausalitätsgründen folgt
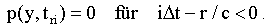
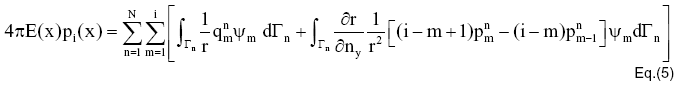
Für jeden Zeitschritt muss die Integration nur über die Schnittmenge der Randelemente Gamman mit einer Hohlkugel durchgeführt werden, welche folgende Abmessungen besitzt; ra = (i-m)cδt und ri=(i-m+1)cδt. Daher sind die resultierenden Matrizen relativ klein.
numerische Validationstests
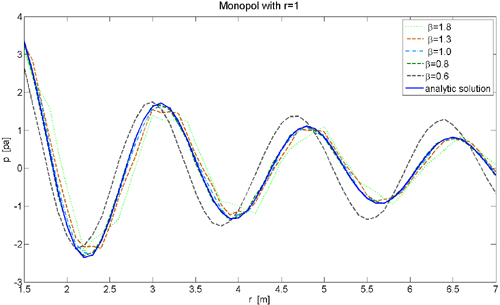
Ein allgemeines Problem der Zeitbereichs-B
Revision der Ergebnisse
Für den Vergleich der transienten BEM mit den Daten aus dem Frequenzbereich werden die Zeitergebnisse mittels FFT in den Frequenzbereich überführt. Die zylindrische Kontrolloberfläche wird in 1376 Elemente verschiedener Größe unterteilt. Daher liegt ß für den gewählten Zeitschritt von 0.1 ms zwischen 1.9 und 2.6 entsprechend der Elementgröße. Dies ist bei Weitem nicht der optimale Wert aber es waren keine anderen Daten aus der LES-Berechnung verfügbar. Trotz des nicht optimalen Verhältnisses aus Zeitschritt und Gitterelementgröße ergaben die Berechnungen stabile Resultate. Abbildung 3 zeigt einen Vergleich der an der H3-Flamme gemessenen Daten mit den Schallleistungsdichten, wie sie jeweils von der transienten BEM und der BEM im Frequenzbereich berechnet wurden.
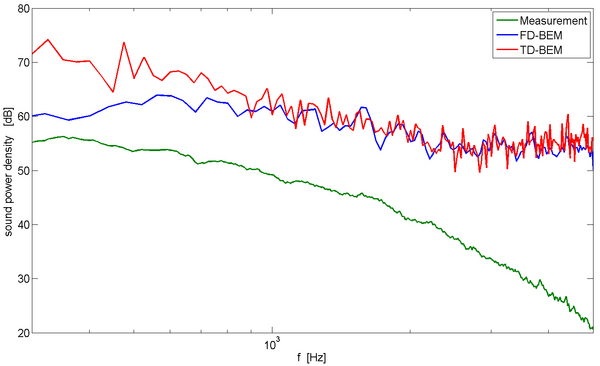
Beide Simulationsergebnisse weichen merklich von dem gemessenen Spektrum ab. Die im betrachteten Frequenzbereich berechneten Schallleistungen sind deutlich zu groß. Eine mögliche Störung der akustischen Berechnungen könnte eine turbulente Schnelleverteilung im Deckelbereich der geschlossenen Kontrolloberfläche sein. Eine weitergehende Diskussion zu Abweichungen zwischen Messungen und Berechnungen kann bei Flemming et al. [10] und Piscoya et al. [11] gefunden werden. Die Ergebnisse beider Berechnungsmethoden sind weitestgehend gleich. Nur im unteren Frequenzbereich bis 1 kHz wird die im Zeitbereich berechnete Schallleistungsdichte überschätzt. Oberhalb der Frequenz von 1 kHz gibt es eine relativ gute Übereinstimmung der Amplituden- und Frequenzcharakteristik.
In radialer Richtung der zylindrischen Kontrolloberfäche ist die Richtwirkung fast omnidirektional und wird hier nicht weiter gezeigt. Abbildung 4 zeigt die Richtwirkung in der Ebene durch den Radius und die Zylinderachse wobei der obere Deckel sich bei 90 ° befindet (siehe Abbildung 2).
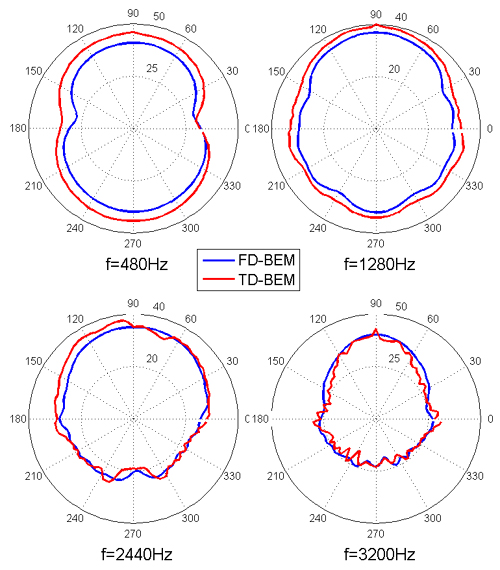
Für hohe Frequenzen strahlt die Flamme zunehmend in Richtung des Deckels. In der Polardarstellung kann wieder eine gute Übereinstimmung zwischen beiden Berechnungen abgelesen werden.
Schlussfolgerungen
Der Vergleich beider Ergebnisse zeigt, dass die abgestrahlte Schallleistung der betrachteten Flamme generell überschätzt wird. Daher sind weitere Optimierungen nötig um eine bessere Vorhersage von Verbrennungslärm zu ermöglichen. Die Berechnungen aus Zeit- und Frequenzbereich stimmen relativ gut überein. Die Abweichungen im unteren Frequenzbereich konnten bisher noch nicht geklärt werden und müssen noch genauer untersucht werden. Der numerische Aufwand im Zeitbereich ist sehr hoch. Für den Fall jedoch, dass sich nur die Werte der Randelemente ändern, z.B. für eine andere Flamme, bei der das Gitter und die Zeitschrittweite gleich bleiben würden, wäre der transiente Ansatz viel schneller, da die Matrizen, die sich aus Gleichung 5 herleiten sich nicht ändern würden und somit wieder verwendbar wären.
