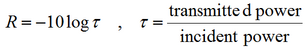The Acoustic Transmission Problem for Plate-like Structures (ATMOS)
The purpose of the DFG projekt ATMOS is the development of three models to compute sound transmission:
- A numerical model for finite thin plates with general properties (including anisotropic, inhomogeneous, profiled plates) and arbitrary (also dissipative) boundary conditions.
- An analytical model for finite, homogeneous, anisotropic plates with dissipative boundary conditions.
- An analytical model for infinite, periodic, profiled plates.
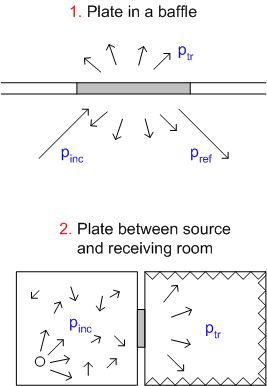
The following two configurations will be investigated
Solution approaches
The calculation of the transmission loss through plates constitutes a fully coupled, fluid-structure-interaction problem. The variables to be determined are usually the displacement of the plate u and the sound pressure p. We consider two ways to compute the transmission loss
Using a direct approach: Is the usual way to handle the problem where
- The coupled system of equations is solved.
- A full populated matrix has to be inverted.
- u and p are computed simultaneously in one step.
Using a physically motivated iteration. In this novel method
- Structure vibration and sound radiation are separately treated.
- u and p are successively improved from an initial guess.
- A sparse matrix has to be inverted to determine u in each step
Basic Equations
Motion of the plate
In the context of a variational formulation, the plate vibrations correspond to extreme values of the sum of the time integrals of the Lagrangian and the work of the external forces. If the displacement of the plate u is expanded in a modal (or polynomial) basis
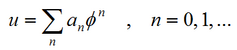
an equation for the coefficients can be derived
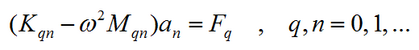
where K is the stiffness matrix, M the mass matrix and F the external force.
Fluid load
The external force acting on the plate is given by
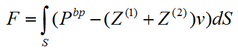
where Z(1) and Z(2) are the radiation impedances, v is the nornal velocity of the plate and Pbp is the "blocked-pressure", i.e. the pressure due to a sound source acting on a rigid plate.
Transmission Loss
The sound transmission is characterized in practice with the Transmission Loss (R)