Die Vorträge finden in Haus Grashof (C) statt.
Können "gierige Verhaltensweisen" zum Ziel führen?
Prof. Dr. Heike Ripphausen-Lipa
(Berliner Hochschule für Technik)
In unserem Alltag lösen wir ständig Optimierungsprobleme wie z.B. eine möglichst kurze Rundreise durch mehrere Städte zu finden, den Kofferraum eines Autos optimal auszunutzen, usw.
Eine typische Vorgehensweise diese Probleme zu lösen ist das sogenannte Greedy-Verfahren oder auch gierige Verfahren. Bei einem Greedy-Verfahren erweitert man eine Teillösung des Problems durch die momentan am günstigsten erscheinende Möglichkeit.
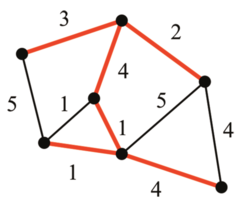
Als Beispiel soll der Aufbau eines Systems von Brücken zwischen mehreren Inseln dienen, sodass man nur über Brücken zwischen den verschiedenen Inseln reisen kann und die Kosten möglichst gering sind. Ein Greedy-Verfahren zum Aufbau eines solchen Systems besteht darin, sukzessiv die kostengünstigste Brücke, d.h. die Brücke kürzester Länge auszuwählen, die nicht überflüssig ist. Dies wird solange wiederholt, bis alle Inseln miteinander verbunden sind.
Es gibt Aufgabenstellungen wie das Bestimmen des Brückensystems mit minimalen Kosten (auch unter dem Namen minimaler Spannbaum bekannt), bei denen Greedy-Verfahren tatsächlich zu einer optimalen Lösung führen. Für andere Aufgabenstellungen, wie z. B. eine kürzeste Rundreise durch Städte zu finden, ist das Greedy-Verfahren jedoch ungeeignet.

Mathematik und Spiele – mit Strategie gewinnen
Maik Pickl
(Freie Universität Berlin)
Spielen ist ein fundamentaler Bestandteil unseres Lebens. Wir lernen durch Spielen und treten dadurch mit Anderen und unserer Umwelt in Beziehung. Und es macht Spaß! Bei vielen Spielen ist nicht nur der Prozess des Spiels wichtig, sondern auch der Ausgang: gewinne oder verliere ich? Natürlich hoffen wir im Spiel auf eine faire Gewinnchance. Aber hat euch nicht auch schon einmal das Gefühl beschlichen, dass bei Spielen wie „Tic-Tac-Toe“ oder „Vier gewinnt“ die Person einen Vorteil hat, die als Erster zieht? Vielleicht kennt ihr ja jemanden, der/die behauptet nie zu verlieren? Wir werden untersuchen, wann und wie es gezielt möglich ist ein Spiel zu gewinnen. Auf der Suche nach solchen Gewinnstrategien werden uns Symmetrien und Copycats begegnen. Mit ein wenig Glück ist es euch danach möglich, durch eine bewusste Anwendung dieser Strategien in Zukunft die Siege der Anderen zu stehlen.

Übernatürliche Zahlen – Zur Unendlichkeit bitte links halten
Alexander Unger
(Humboldt Universität zu Berlin)
Sicher kennen alle Dezimalzahlen mit unendlich vielen Ziffern hinter dem Komma. Aber gibt es auch Zahlen, die unendlich viele Ziffern vor dem Komma haben? Die gibt es! Im Vortrag werden „übernatürliche Zahlen“ vorgestellt. Die haben „nach links“ unendlich viele Ziffern. Auch ohne Komma passiert hier allerhand Merkwürdiges. Während Addieren und Subtrahieren fast wie gewohnt laufen, ist auch Dividieren durch 3 oder 17 ein Klacks. Doch beim Multiplizieren kommt schnell unerwartet 0 heraus, -1 sieht ziemlich groß aus, und 41 ist eine Quadratzahl. Ein bisschen übernatürlich halt.

Maschinelles Lernen ist angewandte Mathematik
Prof. Dr. Frank Haußer
(Berliner Hochschule für Technik)
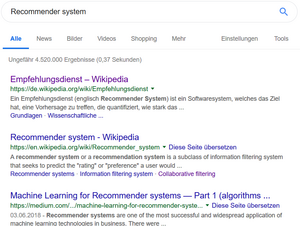
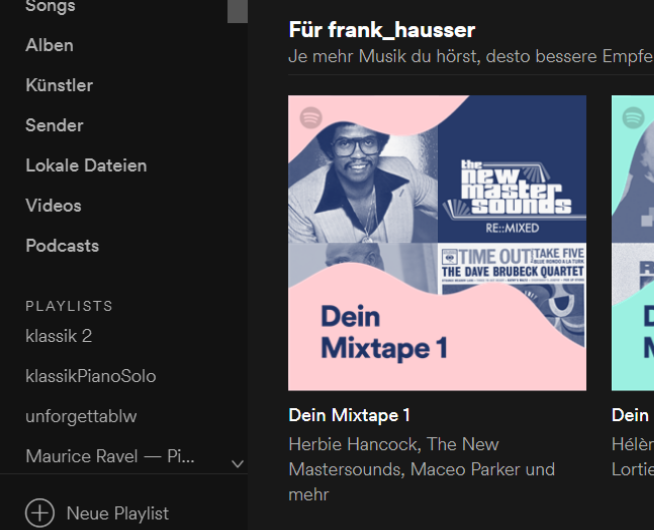
Suchanfragen, Kauf- Film- Musikempfehlungen, Meldungen und Nachrichten in sozialen Netzwerken bis hin zu Online-Dating: Wie funktionieren solche "Recommender Systeme", die uns – manchmal auch ohne dass wir darum gebeten haben – Empfehlungen geben für den nächsten Song, den abendlichen Film, das beste Restaurant oder den idealen Partner? Diese Systeme, die immer mehr mitbestimmen, welchen Ausschnitt der Welt wir wahrnehmen, benutzen Methoden des maschinellen Lernens, die voll von angewandter Mathematik sind.

Die Mathematik hinter der Blockchain
Prof. Dr. Rüdiger Weis, Prof. Dr. Christian Forler
(Berliner Hochschule für Technik)
Unter Blockchain Technologien versteht man eine Mischung aus unterschiedlichen Technologien aus der Informatik und Mathematik, die gewährleistet, dass Daten in einer bestimmten Reihenfolge angeordnet werden. Mit diesem relativ einfachen Grundkonzept kann man Dinge wie eine Buchhaltung realisieren, indem man die Daten in ein öffentlich zugängliches und kryptographisch gesichertes, verteiltes Logbuch schreibt. Der revolutionäre Durchbruch kam mit der Implementierung von Bitcoin als kryptographische Währung. Im ersten Teil unseres Vortrages zeigen wir, dass die Blockchain und digitale Währungen auf recht einfacher Mathematik beruhen und warum gerade dies positive Auswirkungen auf die Sicherheitsanalyse hat. Im zweiten Teil diskutieren wir, welche positive Auswirkungen es gehabt hätte, wenn aktuelle kryptographische Forschungen beim Design einer krytographischen Währung berücksichtigt worder wären.


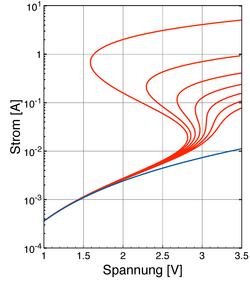
Eine heiße Sache – mit Mathematik elektrothermische Rückkopplung in organischen Leuchtdioden verstehen
Dr. Matthias Liero
(Weierstraß-Institut für Angewandte Analysis und Stochastik Berlin)
Um Vorgänge in der Natur besser zu verstehen oder Prozesse in modernen Technologien zu verbessern, sind mathematische Modelle unerlässlich. Die Simulation solcher Modelle am Computer dient hier oftmals als virtuelles Mikroskop, das es uns erlaubt Effekte sichtbar zu machen, die sonst nur schwer zu erkennen sind. Die Aufgabe eines Mathematikers ist es, die Modelle auf ihre mathematischen Eigenschaften zu untersuchen. Dies beinhaltet den Nachweis der Lösbarkeit und qualitativer Eigenschaften wie zum Beispiel der Positivität von Lösungen und die Einhaltung physikalischer Grundgesetze, aber auch die effiziente numerische Umsetzung in Algorithmen. In diesem Vortrag soll dieses Vorgehen anhand der Modellierung des Zusammenspiels von Wärme- und Stromfluss durch neuartige organische, d.h. auf Kohlenstoff basierende Leuchtdioden demonstriert werden. Hier treten überraschende Effekte auf, wie z.B. S-förmige Strom-Spannungskennlinien mit negativem differentiellen Widerstand. Mit Hilfe des Modells konnten Vorhersagen über das Verhalten der Leuchtdioden gemacht werden, die in anschließenden Experimenten bestätigt wurden.

Das Internet der Dinge – Neue Herausforderungen an die Mathematik
Prof. Dr. Wolfgang König
(Weierstraß-Institut für Angewandte Analysis und Stochastik Berlin/ Technische Universität Berlin)
Auf dem Wege zu drahtlosen Kommunikationsnetzwerken der Zukunft ist noch eine Menge mathematischer Forschung zu bewältigen, insbesondere in der stochastischen Geometrie. Wir geben einen kleinen Einblick in die offenen Probleme und zeigen Lösungsansätze auf. Dabei wird es auch um spannende Phasenübergänge gehen.

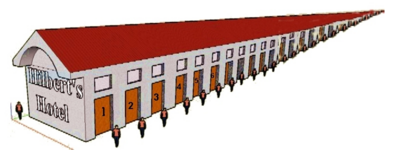
Unendlich klein und unendlich groß – oder warum ein Mathematiker in jedem Hotel Platz findet
Dr. Alexander Fauck
(Humboldt Universität zu Berlin)
Die Vorstellung vom Unendlichen beschäftigt die Menschheit bereits seit den Anfängen der Zivilisation. Doch erst Mitte des 19. Jahrhunderts wurde erstmals eine systematische Untersuchung von Unendlichkeit durch Mathematiker möglich. Dabei zeigte sich, dass es unterschiedlich große Unendlichkeiten gibt und erstaunliche Effekte traten zu Tage. So kann zum Beispiel ein Hotel mit unendlich vielen Zimmern, selbst wenn es voll belegt ist, stets noch neue Gäste aufnehmen. Dieses und andere Phänomene im Zusammenhang mit Unendlichkeit sollen in diesem Vortrag vorgestellt und erläutert werden.
Mathematik des Schwarzfahrens
Dr. Guillaume Sagnol
(Technische Universität Berlin)
Lohnt sich der Kauf einer Fahrkarte? Wir zeigen, wie man mithilfe der Spieltheorie Kontrollen verbessern kann... Oder wie Schwarzfahrer ihren Weg durch das Transportnetz optimieren können!

Wer traut noch dem Computer?
Dr. Martin Weiser
(Zuse Institut Berlin)
Viele Probleme, gerade die praxisrelevanten, lassen sich nur mit Computerhilfe lösen. Dabei spielen uns die Rechenknechte mitunter böse Streiche. Im Vortrag werden wir ein leicht verständliches Verfahren zur Berechnung der Kreiszahl Pi entwickeln, beim Ausrechnen aber eine unangenehme Überraschung erleben. Wer einen Taschenrechner mitbringt, kann sich selbst davon überzeugen. Schließlich untersuchen wir, welche Fallen uns beim Rechnen mit dem Computer erwarten, wie wir sie umgehen können, und welch deutliche Auswirkungen sie bisher in der Welt hatten.

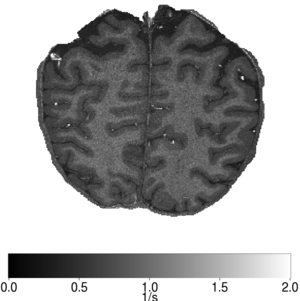
Die Vermessung des Gehirns
Dr. Karsten Tabelow
(Weierstraß-Institut für Angewandte Analysis und Stochastik Berlin)
Die Bildgebung mittels Magnetresonanztomographie hat in den letzten Jahrzehnten den Erkenntnisgewinn in den Neurowissenschaften revolutioniert. Neben strukturellen Bildern mit relativen Bildintensitäten, die durch spezielle Einstellungen der Akquisitionsparameter (Wichtungen) aufgenommen werden, haben kürzlich quantitative Verfahren, also die Messung absoluter physikalischer Parameter an Bedeutung gewonnen. Dazu zählt die Diffusionsbildgebung, welche über richtungsabhängige Diffusionskonstanten Rückschlüsse auf die Zellstrukturen zulässt, aber auch die Relaxometrie. In diesem Vortrag soll ein Einblick in die Möglichkeiten der quantitativen Bildgebung des Gehirns gegeben werden. Dabei kommt es insbesondere auf neue mathematische Verfahren zur Bildverbesserung sowie auf die Verknüpfung verschiedener MR Techniken im Zusammenhang mit biophysikalischen Modellen des Gewebes an.

Chaos und Fraktale in komplexen Systemen
Dr. Rainer Klages
(Technische Universität Berlin)
Was sind komplexe Systeme? Was ist Chaos? Und was sind Fraktale? In meinem Vortrag werde ich diese grundlegenden Begriffe einführen und zeigen, wie sie mathematisch verstanden werden können. Ein wichtiger Teil hierbei ist die mathematische Modellbildung, welche Physik mit Mathematik zusammenbringt. An einem einfachen Beispiel werde ich demonstrieren, dass Chaos in komplexen Systemen fraktale Muster generieren kann.

Perfekte Zahlwörter
Prof. Dr. Steffen Voigtmann
(Berliner Hochschule für Technik)
In der Mathematik werden Zahlen durch Symbole dargestellt. Ein bekanntes Beispiel sind die römischen Zahlen, bei denen I, II, III, IV für die Zahlen 1, 2, 3 und 4 stehen. Schon die Vier zeigt aber, dass u. U. recht komplizierte Muster verwendet werden. Warum ist IV = 4 und IX = 9? Wäre es nicht viel einfacher, den Buchstaben des Alphabets so Zahlen zuzuordnen, dass E+I+N+S = 1, Z+W+E+I = 2, D+R+E+I = 3 usw. gilt? Dann wären auch V+I+E+R = 4 und N+E+U+N = 9 perfekte Zahlwörter, die über sich selbst sprechen. Welche perfekten Zahlwörter gibt es? Kann man vielleicht ein maximales perfektes Zahlwort angeben? Solche und ähnliche Fragen sollen mit elementaren Hilfsmitteln beantwortet werden.

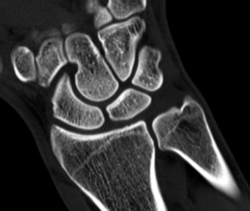
Mathematische Grundlagen der Computertomographie einfach erklärt
Prof. Dr. Yuri Luchko
(Berliner Hochschule für Technik)
Für medizinische Zwecke ist es manchmal erwünscht oder sogar notwendig zu schauen, was im Inneren des menschlichen Körpers passiert. Dabei sind die echten Schnitte eher nicht erlaubt, die Computertomographie (CT) macht es jedoch möglich.
Wie entstehen aber solche CT-Bilder und welche Rolle spielt dabei Mathematik? Die einfachsten mathematischen Modelle der CT führen auf lineare Gleichungssysteme (LGS), die man bereits im Schulunterricht kennenlernt.
Nun sind das aber einerseits LGS mit sehr vielen Variablen, die in der Regel auch noch mehr Gleichungen als Variablen haben. Andererseits sind sowohl die Koeffizienten als auch die rechten Seiten dieser LGS nur aus Messungen bekannt und deswegen fehlerbehaftet.
Im Vortrag klären wir, wie man mit solchen LGS zurechtkommt und geben einen kurzen Ausblick auf fortgeschrittene mathematische Modelle der CT.

Verlust + Verlust = Gewinn: Das Parrondo-Paradoxon
Dr. Stefanie Winkelmann
(Zuse Institut Berlin)
„Das ist nicht fair!“ Solch einen Satz hört man schon von kleinen Kindern, wenn sie sich ungerecht behandelt fühlen. Die meisten Menschen haben ein klares Gespür dafür, wann eine Situation oder ein Spiel für sie fair oder unfair ist. Auf einen Münzwurf, bei dem man entweder einen Euro gewinnt (bei „Kopf“) oder 100 Euro zahlen muss (bei „Zahl“) würde sich wohl kaum jemand einlassen – schließlich ist der im Mittel zu erwartende Verlust viel zu groß. Was aber, wenn man zwei solche Verlustspiele zu einem Gewinnspiel kombinieren kann, indem man sie abwechselnd spielt? Lassen sich dann quasi aus dem Nichts Gewinne erzeugen und man kann beliebig reich werden? In diesem Vortrag werden wir das sogenannte Parrondo-Paradoxon untersuchen, bei dem der Wechsel zwischen unvorteilhaften Situationen tatsächlich Vorteile bringt. Wir definieren den Begriff der Fairness im mathematischen Sinne und zeigen, wie man mithilfe der Mathematik ein wenig Ordnung in die Welt des Zufalls bringen kann. Warum wir trotz allem nicht ins Casino gehen und mit beliebigen Gewinnen rechnen können, wird dabei ebenfalls geklärt.

Mathematik für zerstörungsfreies Prüfen
Dr. Sebastian Götschel
(Zuse Institut Berlin)
Jeden Tag vertrauen wir auf die Zuverlässigkeit unzähliger Dinge: Brücken, Autos, Fahrräder... Damit all diese Sachen nicht plötzlich kaputt gehen, müssen sie während der Herstellung und des Betriebs auf ihre Sicherheit getestet werden. Zerstörungfreies Prüfen ermöglicht es dabei, die Qualität sicherzustellen ohne dass beispielsweise Proben entnommen werden müssen. Wir beschäftigen uns damit, mit mathematischen Methoden aus Messdaten wie dem Temperaturverlauf Rückschlüsse auf die innere, von außen nicht ohne weiteres erkennbare Struktur verschiedener Objekte zu ziehen, Defekte zu finden und ihre Abmessungen zu bestimmen.

Schallwellen in elektronischer Musik
Dr. Michiel Renger
(Weierstraß-Institut für Angewandte Analysis und Stochastik Berlin)
In klassischer Musik kann man Klänge bestimmten Musikinstrumenten zuordnen. Man kann sagen, klassische Musik ist aus den Klängen von Instrumenten zusammengesetzt. In elektronischer Musik geht das eher nicht. Solche Klänge werden mit Synthesizern hergestellt. Aber was für eine Mathematik steckt da eigentlich dahinter? Zu diesem Zweck werde ich eine tiefliegende und wichtige mathematische Theorie besprechen – die Fourieranalyse. Mit ihr kann man Klangwellen in bestimmte Bausteine zerlegen. Danach werden wir sehen (und hören) wie man umgekehrt Klänge aus diesen Bausteinen auf einem Synthesizer konstruieren kann.

Warum spart der Staat Steuern, wenn die Schule eine halbe Stunde früher beginnt? – Eine Einladung zur Diskreten Optimierung!
Prof. Dr. Armin Fügenschuh
(Brandenburgische Technische Universität Cottbus–Senftenberg)
Ein Prototyp schwieriger Optimierungsprobleme ist das Problem des Handlungsreisenden, welches in vielen verschiedenen Anwendungsbereichen eine Rolle spielt: gegeben ist eine große Menge von Städten, und gesucht ist unter allen Touren, die jede Stadt jeweils genau ein Mal besuchen und am Ende wieder am Ausgangspunkt ankommen, eine Tour mit minimaler Gesamtlänge. Mit welcher Art von Mathematik kann dieses Problem erfasst (d.h. modelliert) und gelöst werden? In dem Vortrag wird diese Mathematik vorgestellt. Mit diesem Vorwissen können wir uns dann der Frage zuwenden, warum der Staat Steuern spart, wenn die Schule eine halbe Stunde früher beginnt.