Alle Vorträge finden im Haus Grashof (C) statt. (Lageplan)
ab 13:oo Uhr ab 14:00 Uhr ab 15:00 Uhr ab 16:00 Uhr (Hauptvortrag)
Das Programmheft ist als PDF-Datei verfügbar.
Computertomographie
Dr. Tim Jahn
(Technische Universität Berlin)
⊛ 13:00 Uhr ➤ Ingeborg Meising Saal (ab 7. Klasse)
Stell dir vor, du hättest Superkräfte und könntest durch Wände schauen – aber alles, was du siehst, sind wirre Schatten. Ziemlich unpraktisch, oder? Genau deshalb braucht sogar Superman ein bisschen Mathematik! In der echten Welt übernimmt diese Aufgabe die Computertomographie (CT): Mit Röntgenstrahlen und cleveren Algorithmen verwandeln wir chaotische Daten in gestochen scharfe Bilder. In diesem Vortrag zeigen wir, wie Mathe das Unsichtbare sichtbar macht – ganz ohne Superkräfte.
Mathematik im Alltag am Beispiel von Zahlensystemen
Fedor Romanov
(Weierstraß-Institut für Angewandte Analysis und Stochastik)
⊛ 13:00 Uhr ➤ Raum C20 (ab 7. Klasse)
In diesem Vortrag behandeln wir eine kurze Geschichte der Zahlen und Zahlensysteme sowie die folgenden Arten von Zahlensystemen - binär, dezimal und hexadezimal. Es wird ein Blick auf die Umrechnung von Zahlen zwischen den verschiedenen Zahlensystemen geworfen und es wird erklärt, warum viele moderne Technologien andere Systeme als das Dezimalsystem bevorzugen. Weitere Themen sind Anwendungen von Zahlensystemen in verschiedenen Lebensbereichen wie Computer, Programmierung und alltäglichen oder auch unerwarteten Situationen.
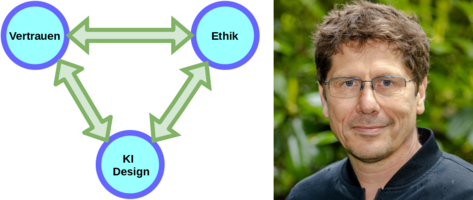
Sechs Arten einer KI zu (miss-)trauen
Prof. Dr. Hanno Gottschalk
(Technische Universität Berlin)
⊛ 13:00 Uhr ➤ Raum C24 (ab 9. Klasse)
Als Gegenbild zu den Allmachtsfantasien, welche des Feld KI oft umgeben, wird das Bild einer vertrauenswürdigen KI beschworen und erforscht. Aber was bedeutet es, dass eine KI vertrauenswürdig ist? Wir nähern uns dieser Frage und sprechen über 6 verschiedene Wege des Ver- oder Misstrauens.
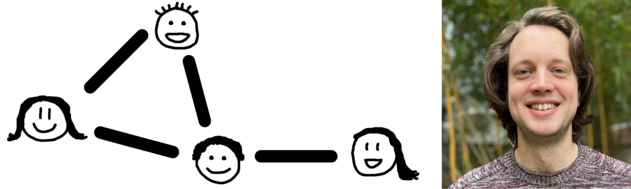
Warum deine Freunde im Mittel mehr Freunde haben als du - eine statistische Kuriosität unter der Lupe
Um die Freundesbeziehungen in einer Gruppe von Menschen darzustellen, können wir die Graphentheorie benutzen. Jede Person stellt einen Knoten im Netzwerk dar, und wir verbinden zwei Personen, wenn sie miteinander befreundet sind. Das kann sich auf digitale soziale Netzwerke in verschiedenen Apps beziehen, oder ganz analog auf die Freundschaften, die wir im persönlichen Kontakt pflegen. Wenn wir uns solche Netzwerke anschauen, tritt ein bemerkenswerter Effekt auf: Es scheint der Fall zu sein, dass die eigenen Freunde mehr Freunde haben als wir selbst – zumindest im Mittel. Interessanterweise kann dieser Effekt allein durch die Struktur von Netzwerken erklärt werden. Wir beleuchten die Gründe dafür und schauen uns unter anderem an, wie dieses Phänomen entsteht und wovon abhängt, wie stark es ausgeprägt ist.

Kleine Fehler, große Wirkung: Von C.F. Gauß zu Klimaprognosen
Vor über 200 Jahren hat Carl Friedrich Gauß die Methode der kleinsten Fehlerquadrate erfunden, um Beobachtungen von Sternen zu analysieren und vorherzusagen. Heute ist sie immer noch eine der wichtigsten Methoden in der statistischen Auswertung experimenteller Daten. Im ersten Teil des Vortrags werden wir mittels Gauß revolutionärer Idee der kleinsten Fehlerquadrate eine Formel für eine Ausgleichsgerade herleiten. Im zweiten Teil werden wir unser neu gewonnenes Wissen benutzen, um ein einfaches Klimamodell für die Erdoberflächentemperatur aus öffentlich zugänglichen Daten zu erstellen und zu diskutieren. Insbesondere werden wir hiermit wichtige wissenschaftliche Aussagen aus den Berichten des Weltklimarats selbst überprüfen.

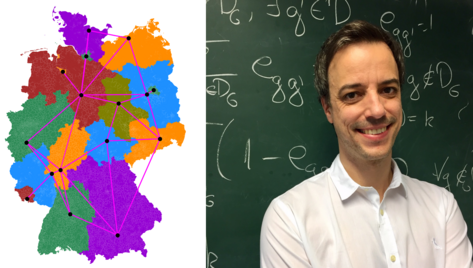
Es wird mir zu bunt - wie Mathematiker Landkarten färben
Prof. Dr. Ralf Lenz
(Hochschule für Technik und Wirtschaft Berlin)
⊛ 13:00 Uhr ➤ Raum C119 (ab 11. Klasse)
Auf Welt- und Landkarten werden Länder häufig farbig dargestellt. Um Grenzen zwischen den Ländern möglichst gut erkennen zu können, sollen dabei stets verschiedene Farben für benachbarte Länder verwendet werden. Doch wie kann man für eine beliebige Karte eine solche Färbung mit möglichst wenig Farben bestimmen ohne alle Kombinationen durchzuprobieren? In diesem Vortrag werden wir diese Aufgabe mathematisch modellieren und anhand eines Praxisbeispiels mit Hilfe des Computers lösen. Zum Schluss betrachten wir die studierte Färbungsmethode noch in einem ganz anderen Kontext. Mit ihrer Hilfe lassen sich nicht nur Landkarten färben, sondern zum Beispiel auch Stundenpläne in Schulen erzeugen.
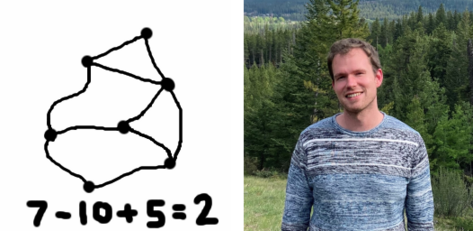
Euler's Polyedersatz
Fabian Lehmann
(Humboldt-Universität zu Berlin)
⊛ 14:00 Uhr ➤ Ingeborg Meising Saal (ab 7. Klasse)
Ein Polyeder ist eine Verallgemeinerung von geometrischen Objekten wie Würfel und Pyramide. Die zentrale Aussage über Polyeder ist die Euler'sche Polyederformel: sie setzt die Azahl der Ecken, Kanten und Flächen eines Polyeder in Beziehung. Wir werden sehen, dass man daraus verblüffende Folgerungen ziehen kann: 1. Eine mathematisch Erklärung, dass man einen Luftballon nicht ohne Schere in einen Schwimmring umformen kann. 2. Im Spiel "Brussels Sprouts" steht der Ausgang schon zu Beginn fest. 3. Wenn man einen Igel kämmt, gibt es immer einen Wirbel.
Welch ein Zufall...!?
Dr. Stefanie Winkelmann
(Zuse Institut Berlin)
⊛ 14:00 Uhr ➤ Raum C20 (ab 7. Klasse)
Zufall begegnet uns überall – beim Würfeln, in Spielen oder sogar im Alltag. Aber was steckt wirklich dahinter? In diesem Vortrag erforschen wir, was Zufallsexperimente sind, wie Ereignisse voneinander abhängen (oder eben nicht) und warum das Gesetz der großen Zahl so wichtig ist. Außerdem nutzen wir Computersimulationen, um Dinge zu schätzen, die sich nicht so einfach berechnen lassen. Sei dabei und finde heraus, wie Mathematik den Zufall durchschaubar macht!
Umsteigen ohne Warten - Mathematische Fahrplanoptimierung
Dr. Niels Lindner
(Freie Universität Berlin)
⊛ 14:00 Uhr ➤ Raum C24 (ab 9. Klasse)
Wir erklären den Einsatz mathematischer Methoden in der Verkehrsplanung. Der Fokus liegt dabei auf dem Modellieren und Optimieren von Taktfahrplänen, wie sie bei vielen Verkehrsunternehmen eingesetzt werden. Dies führt zu einem interessanten Optimierungsproblem, das zahlreiche Facetten der Graphentheorie und der kombinatorischen Optimierung beinhaltet. Auf der praktischen Seite ist das Paradebeispiel die mathematische Optimierung des Berliner U-Bahn-Fahrplans, bei der verglichen mit der manuellen Planung sogar ein Zug eingespart werden konnte.
Aus Beobachtungen logische Regeln lernen
Viele kennen heute die "künstliche Intelligenz" als ein brauchbares, vereinfachtes mathematisches Modell unseres "Denkens". Es wird gesagt, sie sei in der Lage, Regeln aus Beobachtungen zu erlernen. Geht das überhaupt? In der Geschichte hat es verschiedene Ansätze zur Mathematisierung des Denkens gegeben. Gottfried Wilhelm Leibniz zum Beispiel benutzte im Jahr 1679 sogenannte "charakteristische Zahlen" zur Mathematisierung der antiken Logik von Aristoteles (ca. 350 v. Chr. "Organon"). Leibniz hoffte vergeblich, alle logischen und philosophischen Streitfragen mit Hilfe des Rechnens mit diesen Zahlen lösen zu können. George Boole greift in seinem Buch "The Laws of Thought" (Die Gesetze des Denkens, 1854) diesen Ansatz auf und erfindet eine mathematische Struktur, die auch heute noch in Rechnern für das automatisierte Durchführen logischer Schlussfolgerungen verwendet wird. Geht man gedanklich den Weg von Aristoteles, Leibniz und Boole (so wie es Karl Popper 1934 in "Logik der Forschung" getan hat), dann kommt man zu dem Schluss, dass man nicht logische Regeln aus Beobachtungen ableiten kann, sondern dass "Beobachtungen logische Regeln zerstören".

Mathematik beim Frühstück: Wie schnell kühlt sich mein Kaffee ab und was Newton damit zu tun hat
Viele Erscheinungen, die uns im Alltag begegnen, können mit mathematischen Modellen beschrieben, verstanden und erklärt werden. Im Vortrag werden wir uns mit einem aus dem Alltag bekannten Problem beschäftigen, und zwar, wollen wir die Zeit berechnen, die unser Frühstückkaffee benötigt um sich bis zur Trinktemperatur abzukühlen. Es ist das Verdienst von einem der berühmtesten Naturwissenschaftler aller Zeiten Sir Isaac Newton, hinter der kontinuierlichen Abnahme der Temperatur eines heißen Gegenstandes eine Gesetzmäßigkeit zu vermuten und nachzuweisen. Heutzutage bezeichnet man diese Gesetzmäßigkeit als das Newtonsche Abkühlungsgesetz. Im Vortrag diskutieren wir zuerst ein einfaches mathematisches Modell der Abkühlung einer Tasse mit heißem Kaffee, das auf der Grundlage des Newtonschen Abkühlungsgesetzes in Form einer iterativen Folge aufgestellt wird. Um die Genauigkeit der Vorhersagen dieses Modells zu erhöhen, wird draus ein etwas komplizierteres Modell in Form einer Differentialgleichung hergeleitet. Anschließend besprechen wir unter anderem wie die beiden Modelle zusammenhängen und was die Ergebnisse, die mit ihrer Hilfe berechnet werden, mit Realität zu tun haben.

Chaos, Schönheit und Finanzen - Mathematik als universelle Sprache
Dr. Christian Finke
(d-fine GmbH)
⊛ 14:00 Uhr ➤ Raum C119 (ab 11. Klasse)
Seit dem Altertum versucht eine kleine Gruppe von Mathematikern immer wieder, ein gewisses x in Gleichungen zu finden. In der heutigen Schule darf und muss das nun jeder Schüler, woraus man eine gewisse Wichtigkeit ableiten könnte. Wir unternehmen eine Reise durch die Geschichte der Gleichungssysteme, wollen verstehen, warum sie seit Urzeiten so wichtig sind und warum sie heute im Zentrum von Raumfahrt, Neurobiologie und Wettervorhersagen stehen. Dass nichtlineare Gleichungssysteme seit dem Aufkommen von Computern auch optisch faszinierend sind, nehmen wir als zusätzliche Motivation gern mit schauen uns an, was bunte Bilder uns über die Funktionsweise der Welt verraten.
Das Haus vom Nikolaus und der kürzeste Schulweg: Ein Ausflug in die Graphentheorie
Kann man eine Figur in einem Zug zeichnen, ohne den Stift abzusetzen und ohne eine Linie doppelt zu zeichnen? Diese Frage führt uns direkt in die spannende Welt der Graphentheorie. Wir starten mit dem berühmten Königsberger Brückenproblem und entdecken, wie der Mathematiker Leonhard Euler vor fast 300 Jahren eine völlig neue Art der Mathematik begründet hat. Danach wenden wir das Gelernte auf bekannte Zeichnungen an und klären, warum manche Figuren sich leicht in einem Zug zeichnen lassen – und andere nicht. Doch Graphentheorie kann noch mehr: Sie hilft uns auch, den kürzesten Weg von A nach B zu finden. Anhand von einfachen Beispielen erarbeiten wir gemeinsam, wie solche Probleme gelöst werden – und wo diese Mathematik in unserem Alltag steckt. Der Vortrag richtet sich an Schülerinnen und Schüler der 7. und 8. Klasse und erfordert keine mathematischen Vorkenntnisse – nur Neugier und Lust am Entdecken!

Wer wird Haribillionär?
Julian Kern
(Freie Universität Berlin)
⊛ 15:00 Uhr ➤ Raum C20 (ab 7. Klasse)
Willst du herausfinden, wie man bei einem Ratespiel erfolgreich sein kann? Dann begleite uns zum Workshop "Wer wird Haribillionär"! Hier lernst du, wie dir die Wahrscheinlichkeitsrechnung dabei hilft, mehr Haribo-Preise zu gewinnen. Wir werden gemeinsam das Geheimnis des Ziegenproblems lüften und dir zeigen, wie du zum Meisterstrategen wirst. Sei dabei und werde zum Haribillionär!
Wer traut noch dem Computer?
Dr. Martin Weiser
(Zuse Institut Berlin)
⊛ 15:00 Uhr ➤ Raum C24 (ab 9. Klasse)
Viele Probleme, gerade die praxisrelevanten, lassen sich nur mit Computerhilfe lösen. Dabei spielen uns die Rechenknechte mitunter böse Streiche. Im Vortrag werden wir ein leicht verständliches Verfahren zur Berechnung der Kreiszahl Pi entwickeln, beim Ausrechnen aber eine unangenehme Überraschung erleben. Wer einen Taschenrechner mitbringt, kann sich selbst davon überzeugen. Schließlich untersuchen wir, welche Fallen uns beim Rechnen mit dem Computer erwarten, wie wir sie umgehen können, und welch deutliche Auswirkungen sie bisher in der Welt hatten.
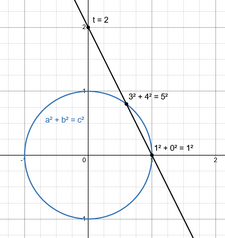
Diophantische Gleichungen mit Geometrie lösen
Theo Müller
(Humboldt-Universität zu Berlin)
⊛ 15:00 Uhr ➤ Raum C113 (ab 9. Klasse)
Diophantische Gleichungen - Gleichungen, für die nur ganzzahlige Lösungen gesucht werden - sind eines der weitesten und grundlegendsten Probleme in der Zahlentheorie. Eine diophantische Gleichung deren Lösung bereits im alten Griechenland bekannt war, ist a² + b²= c². Sie fragt nach Pythagoreischen Tripeln: rechtwinkligen Dreiecken, deren drei Kantenlängen alle ganze Zahlen sind. Machen wir aber aus der 2 eine 3, erhalten wir die Gleichung a³ + b³ = c³, die um ein Vielfaches schwerer ist. Die allgemeine Form der Gleichung, a^n + b^n = c^n, wird durch den Großen Fermatschen Satz gelöst, der erst vor 30 Jahren durch große mathematische Durchbrüche bewiesen wurde. Beim Lösen von Gleichungen ist es leicht, sich in den vielen Variablen und Termen zu verlieren. Daher soll es in diesem Vortrag darum gehen, wie diophantische Gleichungen durch Geometrie anschaulich gemacht, und sogar gelöst werden können. So wird eine Gleichung zu einer geometrischen Form, und eine Lösung zu einer geometrischen Konstruktion. Durch die Brille der Geometrie können wir erkennen, wie die klassische Klassifikation aller Pythagoreischen Tripel auf andere diophantische Gleichungen angewandt werden kann, oder was die Gleichung a³ + b³ = c³ so viel schwerer als a² + b² = c² macht.
Perkolationstheorie - Kaffeekochen aus stochastischer Sicht
Dr. Lukas Lüchtrath
(Weierstraß-Institut für Angewandte Analysis und Stochastik)
⊛ 15:00 Uhr ➤ Raum C116 (ab 11. Klasse)
Kochen wir Kaffee, kippen wir heißes Wasser in einen mit Kaffeepulver gefüllten Filter. Das Wasser sucht sich dann einen Weg durch das Pulver und tropft unten als Kaffee in die Tasse. Je dichter das Pulver in dem Filter ist, desto schwieriger ist es für das Wasser einen Weg durch das Pulver zu finden. Aber wie wahrscheinlich ist es, dass das Wasser überhaupt einen Weg findet und sich nicht irgendwo im Filter aufstaut? Mit Fragen dieser Art beschäftigt sich die Perkolationstheorie (engl. to percolate: durchsickern). Dabei wird der Filter als Graph modelliert. Ein Graph besteht aus Knotenpunkten und Verbindungskanten zwischen diesen. Die Interpretation ist, dass Wasser von einem Knotenpunkt zum anderen sickern kann, wenn es zwischen beiden eine Verbindungskante gibt. In dem Vortrag betrachten wir Graphen, in denen die Knotenpunkte gitterförmig angeordnet sind. Jeder Knotenpunkt ist zu jeden seiner benachbarten Gitterpunkte mit einer gewissen Wahrscheinlichkeit verbunden. Schon in dieser recht einfachen Struktur lassen sich interessante Effekte beobachten, abhängig von der Verbindungswahrscheinlichkeit. Wir werden einige dieser Effekte kennen lernen und auch die oben genannte Frage beantworten.

Die Welt (zu beschreiben) verstehen mit Mathematik
Julian Hille
(Freie Universität Berlin)
⊛ 15:00 Uhr ➤ Raum C119 (ab 11. Klasse)
"Funktionen, Ableitungen, Mathematik - das brauche ich sicher nie wieder!", denken sich viele Schüler*Innen. Dabei bauen die Werkzeuge, mit denen wir die Welt um uns herum zu verstehen versuchen, auf genau diesen Konzepten auf. Wir brauchen sie also in Wahrheit immer und überall. So auch bei der Beschreibung der Teilchen, aus denen unsere Welt aufgebaut ist.
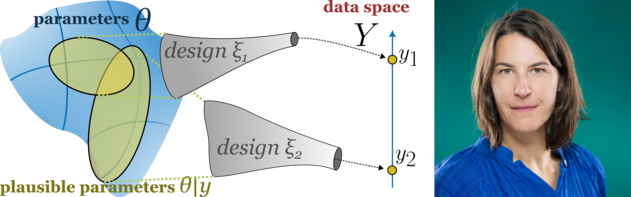
Optimal Experimental Design – Mehr Erkenntnisse durch clevere Experimente
Wie kann man durch gezielte Planung von Experimenten mehr Erkenntnisse gewinnen, ohne unnötig viele Versuche durchzuführen? In diesem Vortrag geben wir eine Einführung in das Konzept des „Optimal Experimental Design“, das in Wissenschaft und Industrie genutzt wird, um Experimente so zu gestalten, dass mit minimalem Aufwand maximale Informationen gewonnen werden. Anhand anschaulicher Beispiele entwickeln wir Strategien, um den Informationsgewinn zu maximieren, und beleuchten Methoden, mit denen sich die besten Versuchspläne gezielt finden lassen. Abgerundet wird der Vortrag durch spannende Anwendungsbeispiele aus der Praxis, die verdeutlichen, wie optimal gestaltete Experimente komplexe Zusammenhänge aufdecken und Innovationen vorantreiben können.