Thin baffled plate
A thin rectangular plate of sides Lx and Ly is placed in an infinite rigid wall. The baffle divides the space in two halves, below and above the wall. A plane wave in one side of the plate is considered. The incident pressure induces bending waves on the plate. The vibration of the plate produces sound radiation in both halfspaces.
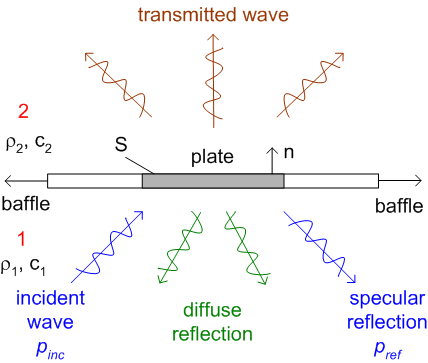
Direct approach
Semi-analytical method
A polynomial basis of the form
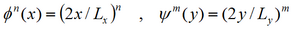
is chosen. The displacement of the plate is given by
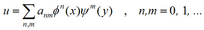
The boundary conditions of the plate are introduced in the system by means of a matrix added to the stiffness matrix K=Kplate + Kbound.
The matrices K and M can be computed analytically. The radiation impedances Z(1) and Z(2) are expressed as infinite series and the source term Pbp is obtained using recurrence relations.
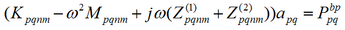
Finite element / boundary element method
The plate and the differential equations are discretized. The physical quantities (e.g. pressure, displacement) are calculated in a finite number (N) of points on the structure (nodes). To reduce the size of the system, the basic equations can be transformed from nodal coordinates to modal coordinates. Usually, a modal basis with the eigenvalues and eigenvectors of the plate in vacuum (dry modes) is used. The displacement vector is defined as
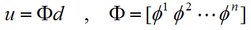
where d is the vector of modal amplitudes. The vectors u and d are related through a N×n matrix (n<N) made up of the first n eigenvectors.
The modal amplitudes are obtained solving the equation
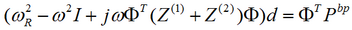
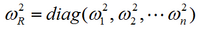
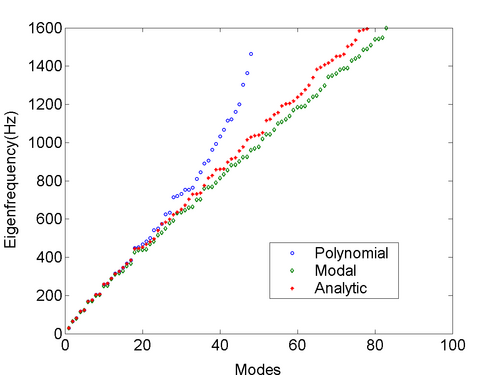
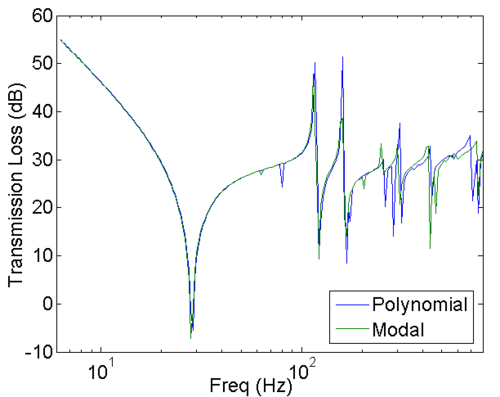
Example: Simply supported plate
The modes and the transmission loss of a thin simply supported steel plate using both direct methods are compared.
The eigenmodes and eigenfrequencies of a simply supported plate are given by
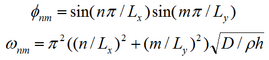
with D=Eh3/12(1-v2), E=Young's modulus and v=Poisson's ratio
Iterative Method
Starting from the blocked-pressure approximation, the displacement of the plate is successively improved through a combination of separate calculations of structure-borne and air-borne sound until a sufficiently accurate value is reached.
The n-th double step of the procedure reads
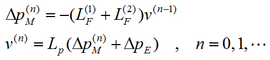

Start of the iteration:
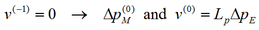
Results
Near the eigenfrequencies, the values of the transmission loss diverge, while the values converge for all other frequencies. The reason for the divergence lies on the fact that the operator Lp becomes singular near the eigenfrequencies by vanishing damping.
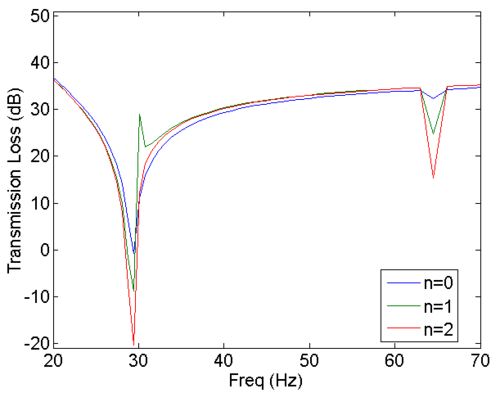
Splitting method to improve convergence
Adding and subtracting an auxiliary matrix ZA to the basic equations, a new iteration scheme can be built
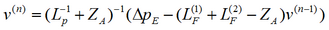
A proper ZA needs to be found. A very convenient choice is the one that makes Zn=Lp-1+ZA a diagonal matrix. Taking the diagonal elements of Zn equal to the radiation impedance of an infinite panel reduces the spectral radius just below 1 assuring convergence but with a very slow rate.
Publications
[Pis09a] R. Piscoya, M. Ochmann, Numerical prediction of sound transmission through shells and plates,
Proc. ICSV16, Poland, 2009. [pdf]
[Pis09b] R. Piscoya, N. Gorenflo, M. Ochmann, Benchmarking for the numerical prediction of sound
transmission through slits, plates and shells, Proc. ICTCA, Germany, 2009. [pdf]
[Pis10a] R. Piscoya, M. Ochmann, Berechnung der Schalldämmung endlicher Platten durch eine
Kombination von numerischer Modalanalyse und BEM, Proc. DAGA, Germany, 2010. [pdf]
[Pis10b] R. Piscoya, Y. Aoki, M. Ochmann, W. Maysenhölder, Methoden zur Berechnung der
Schalldämmung dünner Platten, Proc. DAGA, Germany, 2010. [pdf]
[Pis10c] R. Piscoya, M. Ochmann, Calculation of the transmission loss of finite plates using numerical
modal analysis and BEM, Proc. ICSV17, Egypt, 2010. [pdf]
[Pis10d] R. Piscoya, Y. Aoki, M. Ochmann, W. Maysenhölder, Different methods for computing the sound
transmission through finite, thin plates, Proc. ICSV17, Egypt, 2010. [pdf]
